Photometric Stereo

1 从明暗恢复形状

从明暗恢复形状（Shape from Shading，SfS）是指从图像的明暗信息推断出物体表面几何形状的过程。这个问题假设光照条件已知，目标表面是光滑且均匀的，并且照明是单向的。其基本思想是根据目标表面对光照的反应，推断出表面法线，从而得到表面的三维形状。

1.1 渲染方程

渲染方程为：

$$L_o(\mathbf{x}, \omega_o) = L_e(\mathbf{x}, \omega_o) + \int_{\Omega} f(\mathbf{x}, \omega_i, \omega_o) L_i(\mathbf{x}, \omega_i) (\mathbf{n} \cdot \omega_i) d\omega_i$$

我们将其简化：

$$L_{\text{out}} = \rho \cdot L_{\text{in}} \cdot n^\top s = R(n)$$

• $L_{\text{out}}$ ：表示出射光线
• $\rho$ ：表示该点的漫反射率
• $L_{\text{in}}$ ：表示入射光线
• $n$ ：表示表面法线

1.2 梯度空间表示法

梯度空间表示法 Gradient Space Representation，使用梯度信息来表示物体表面的几何形状。

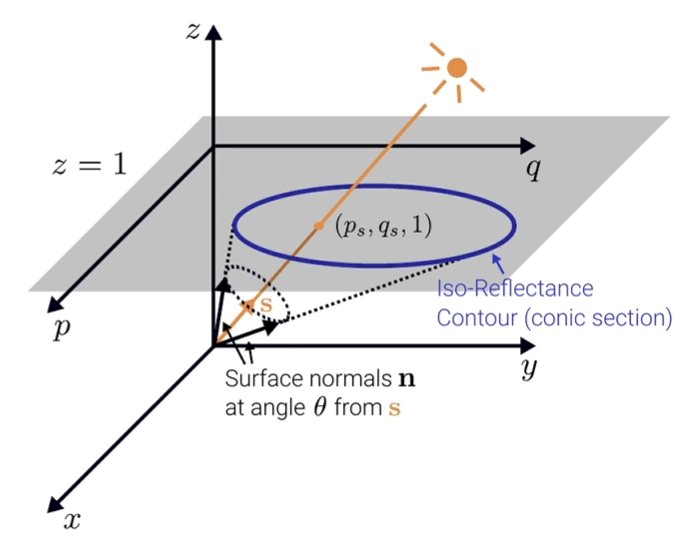
在梯度空间表示法中，给定光线 $s$ 和观察到的反射率 $R$，我们可以通过以下方式来计算法线 $n$：

1. 计算 $n^\top s = \cos(\theta)$，得到 $\theta$ —— 法线 $n$ 与光线 $s$ 之间的夹角
2. 按照给定的角度 $\theta$，从光线 $s$ 开始，投影这个集合到 $z = 1$ 平面上，我们可以得到一个锥面曲线即反射率曲线 Iso-Reflectance Contour，它表示出了所有与 $s$ 的夹角为 $\theta$ 的可能法线

通过不同的反射率 $R$ ，我们可以得到反射率图（Reflectance Map）：

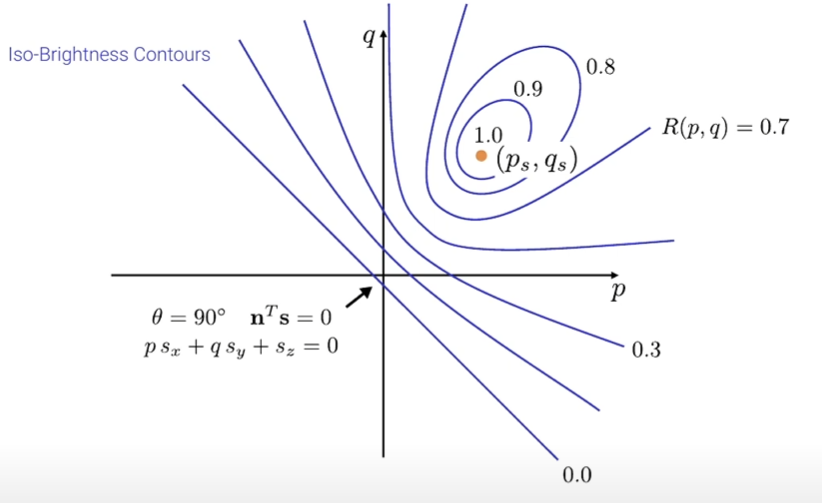
因此，在梯度空间表示法中，我们可以通过结合反射率图和其他几何信息来有效地参数化法线，并利用这些信息来推断物体表面的形状和材质。

2 光度立体法

光度立体法（Photometric Stereo）是通过在相同视点但采用不同（已知）点光源的多张图像来实现三维重建的。其需要对每个像素的法线和反射率进行估计。

2.1 采集 K 张图像

在相同的相机视点下，采集 K 张图像，每张图像使用不同的已知点光源。这些光源的位置和方向应该是已知的，并且在不同的图像中有所变化。

通过如下的反射率图可以看到，对于每个像素，我们必须要有3个反射率图才能确定一个真正的法线，所以，我们至少要有从3个不同的方向来的光源

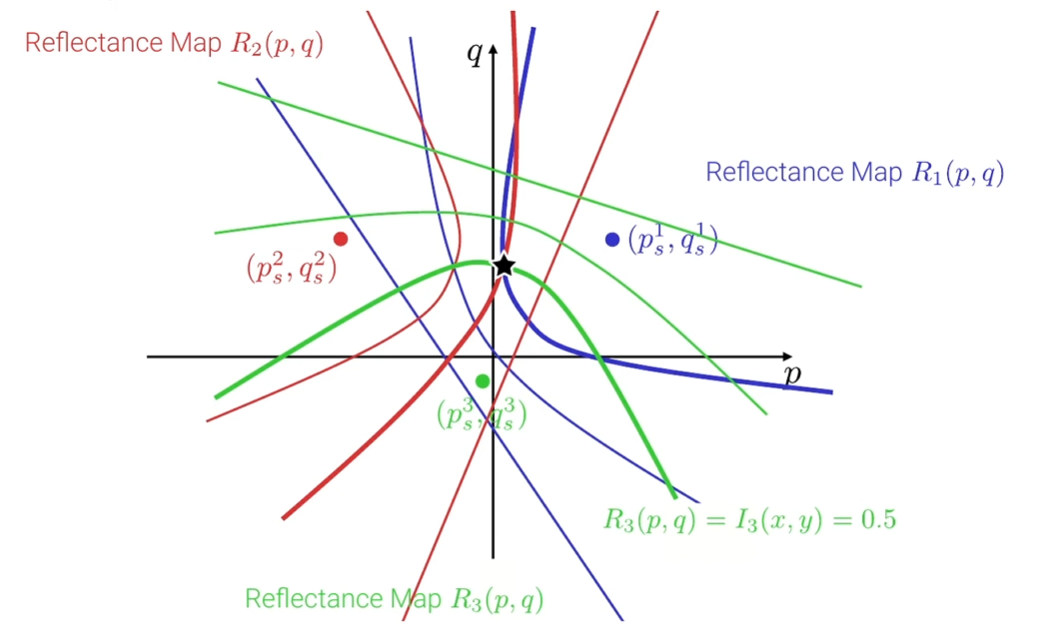
但是要避免共线光源：当光度立体设置中使用的所有光源都是共线时（位于同一直线或平面上），所得的线性系统将变得秩亏。这使得不可能唯一地确定每个像素的表面法线。因此，光度立体无法提供准确的重建。

2.2 光度法线与反射率估计

对于每个像素，利用 K 张图像中的光照信息，通过解光度立体方程组来估计法线和反射率：

使用兰伯反射，并且入射光强度为 $L_{\text{in}} = 1$，那么图像的亮度 $I$ 可以表示为：

$$I = L_{\text{out}} = \rho \cdot n^\top s = \rho \cdot s^\top n$$

对于给定的三个观测（相同的 $v$，不同的 $s$），我们可以将其表示为矩阵形式如下：

$$\begin{bmatrix} I_1 \\ I_2 \\ I_3 \end{bmatrix} = \begin{bmatrix} s_1^\top \\ s_2^\top \\ s_3^\top \end{bmatrix} \cdot \rho \cdot n$$

其中，$I_1, I_2, I_3$ 分别是三个观测得到的图像亮度， $s_1, s_2, s_3$ 分别是对应的三个光源方向向量，$\rho$ 是漫反射率，$n$ 是法线向量。

通过使用更多的光源可以获得更好的结果（通过对测量进行平均）。通过最小二乘解法我们得到：

$$\rho n = (S^\top S)^{-1}S^\top I$$

其中，$S$ 是包含所有光源方向 $s_i$ 的矩阵，$I$ 是包含对应图像亮度 $I_i$ 的向量

得到 $\rho n$ 后，可以通过 $\rho = ||\rho n||_2$ （ $n$ 是单位向量 ）来计算漫反射率 $\rho$ ， $n = \rho n / \rho$

简单实现代码如下：

def compute_normals_albedo_map(imgs, mask, light_positions):
    """
    imgs np.array [k,h,w] np.float32 [0.0, 1.0]
    mask np.array [h,w] np.bool
    light_positions np.array [k,3] np.float32
    ---
    dims:
    k: number of images
    h: image height (num rows)
    w: image width (num cols)
    """

    S = light_positions
    I = imgs.reshape(imgs.shape[0], -1)

    # rho n = (S^T S)^-1 S^T I
    rho_n = np.linalg.inv(S.T @ S) @ S.T @ I
    # rho = ||rho_n||
    rho = np.linalg.norm(rho_n, axis=0)
    # n = rho_n / rho
    n = np.divide(rho_n, rho, out=np.zeros_like(rho_n), where=rho != 0)

    # mask out
    mask_flat = mask.flatten()
    n[:, ~mask_flat] = 0

    normals_unit = n.T.reshape(imgs.shape[1], imgs.shape[2], 3)
    rho = rho.reshape(imgs.shape[1], imgs.shape[2])

    assert normals_unit.shape == (imgs.shape[1], imgs.shape[2], 3)
    assert rho.shape == (imgs.shape[1], imgs.shape[2])

    rho = np.clip(rho, 0.0, 1.0)
    normals_unit = np.clip(normals_unit, 0.0, 1.0)

    return normals_unit, rho, mask

输出是：

• normals_unit：三维数组，表示每个像素点的单位法线向量。它的形状是 (imgs.shape[1], imgs.shape[2], 3)，其中 imgs.shape[1] 和 imgs.shape[2] 分别是图像的高度和宽度，3 表示每个像素点的法线有三个分量（x、y、z）
• rho：二维数组，表示每个像素点的漫反射率。它的形状是 (imgs.shape[1], imgs.shape[2])，与图像的大小相同，对应每一个像素的反射率

2.3 重新照亮场景

我们现在知道整个图像的像素法线和反照率，这使我们能够重新照亮场景（即人为地改变灯光位置）

def relight_scene(light_pos, normals_unit, albedo, mask):
    """
    light_pos np.array [k,3] np.float32
    mask np.array [h,w] np.bool
    ----
    dims:
    h: image height (num rows)
    w: image width (num cols)
    ----
    returns:
        imgs np.array [h,w] np.float32 [0.0, 1.0]
    """
    assert light_pos.shape == (3,)
    assert np.allclose(1.0, np.linalg.norm(light_pos))
    assert normals_unit.shape[-1] == 3
    assert len(normals_unit.shape) == 3

    img = albedo * (normals_unit @ light_pos)
    # mask out
    img[~mask] = 0
    img_norm = np.clip(img, 0.0, 1.0)

    assert np.all(
        np.logical_and(0.0 <= img_norm, img_norm <= 1.0)
    ), "please normalize your image to interval [0.0,1.0]"
    return img_norm

其接受灯光位置、像素法线、反射率和掩码作为输入，并返回重新照亮后的图像。

其实其中核心就是：根据之前的简化的渲染公式 $L_{\text{out}} = \rho \cdot L_{\text{in}} \cdot n^\top s$ ，其中设置入射光线为1，即可得：

img = albedo * (normals_unit @ light_pos)

Marching Cubes

1 体积融合 Volumetric Fusion

将多个视角的结果融合在一起形成一个完整的对象或场景的三维表示。主要包括以下三个步骤：

1. 深度到SDF转换：从获取的深度信息被转换为有符号距离函数（SDF）。SDF表示空间中每个点到被重建对象的最近表面的距离。距离的符号（+/-）表示点是在表面内部还是外部。
2. SDF体积融合：将多个融合成一个场景的单个体积表示，将来自不同视角的深度测量集成到一起。
3. 网格提取：一旦获得了体积表示，最后一步就是提取多边形网格，重建对象的表面，即从SDF重新转换回去。使用 Marching Cubes 算法。

2 SDF体积融合

使用有符号距离函数（SDF）融合，通过计算每个体素的加权平均来生成场景的全面表示。在每个迭代中将来自不同视角的新深度测量数据整合进来，逐渐更新每个体素的融合权重（W）和距离（D）值：

$$D_{i+1}(x) = \frac{{W_{i}(x) \cdot D_{i}(x) + W_{i+1}(x) \cdot d_{i+1}(x)}}{{W_{i}(x) + w_{i+1}(x)}}$$

$$W_{i+1}(x) = W_{i}(x) + w_{i+1}(x)$$

其中：

• $D_{i}(x)$ 是当前迭代中体素 x 的融合距离值。
• $W_{i}(x)$ 是当前迭代中体素 x 的融合权重值，即来自所有相机的权重之和。
• $d_{i+1}(x)$ 是来自新相机 i+1 的新深度测量数据在体素 x 处的距离值。
• $w_{i+1}(x)$​ 是分配给来自新相机 i+1 的新深度测量数据的权重。

权重：

1. 降低表面后面的SDF值：有时可能存在表面后面的区域，这些区域在采集数据时没有被观测到。
2. 降低不太确定的射线的权重：某些射线可能由于距离较远、方向不明确或位于物体边界附近而具有较低的可信度。

3 网格提取

这里使用 Marching Cubes 算法进行网格提取。从有符号距离函数（SDF）中提取网格，步骤如下：

1. 确定零水平集：零水平集代表对象的表面，即SDF等于零的地方。这就是提取三角形网格的地方。

2. 估计拓扑结构：

   • 对于每个与表面相交的单元格，根据符号变化的配置估计拓扑结构
   • 不同的符号变化配置对应于单元格内部的不同三角形排列。在3D中有256种可能的拓扑结构（8个点有或无，即2^8）

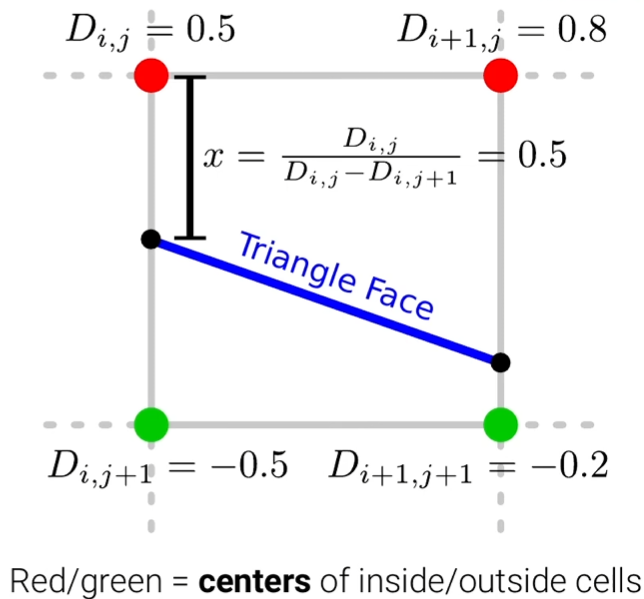
3. 预测顶点位置：

   • 顶点通常位于线性插值函数的零交叉点处，该函数为 $f(x) = D + x(D' - D)$，其中 $D$ 和 $D'$​ 分别是单元格顶点处的SDF值。

     # avoid divison by zero
     if sdf_val_at_x1 == sdf_val_at_x2:
         crossing_location = (loc_x2 + loc_x1) / 2
     else:
         crossing_location = loc_x1 + (0 - sdf_val_at_x1) * (loc_x2 - loc_x1) / (sdf_val_at_x2 - sdf_val_at_x1)

   • 使用线性插值来估计沿着单元格边缘的零交叉点顶点的精确位置。