ex3 Probabilistic Graphical Models
约 2202 字大约 7 分钟
2024-11-24
1 马尔可夫随机场
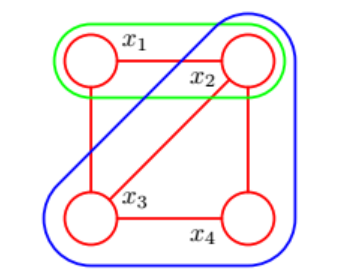
马尔可夫随机场(Markov Random Field,MRF),是概率无向图模型的一种,用于描述变量之间的关系,其中变量之间的连接是无向的。
MRF的结构和条件独立性质是基于团块和最大团块的概念来定义的。
团块是图中结点的子集,其中子集中的节点两两之间都直接连接,而最大团块则是不能再添加其他节点而保持两两连接的最大子集。
MRF的联合概率分布可以表示为:
P(x)=Z1C∏ψC(xC)
其中,
- P(x) 是联合概率分布
- Z 是归一化常数
- ψC(xC) 是势函数,表示团块 C 中的变量组合 xC 的势能
2 因子图
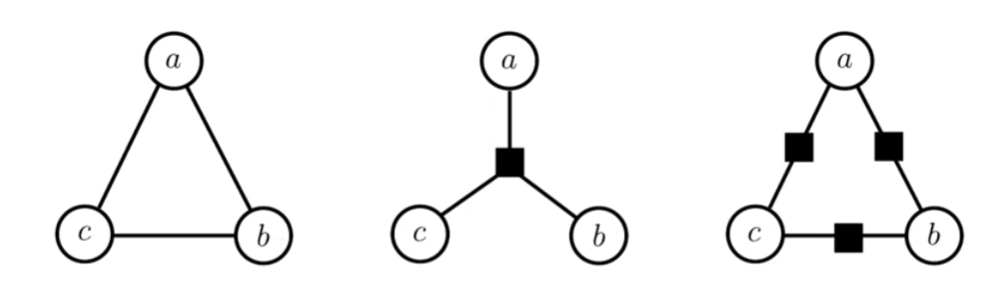
上面三个都代表同一个MRF,后面两个是该MRF的因子图,不同的因子图代表着不同的分解:
- 第一个: P(a,b,c)=Z1f(a,b,c)
- 第二个: P(a,b,c)=Z1f1(a,b)f2(b,c)f3(a,c)
代表因子 f 的结点与代表变量 xi 的边缘(或半边缘)相连,当且仅当 f 是关于 xi 的函数
3 置信度传播
置信度传播算法(Belief Propagation,BP)是一种用于计算概率图模型中的边缘概率分布或**最大后验概率(MAP)**估计的近似推断算法。它基于因子图结构,通过在因子图上传递消息来计算变量之间的联合概率分布。
最大后验概率:最大后验概率即在给定观测数据 D 的情况下,使后验概率最大化的参数或隐含变量值。通常表示: θ^MAP=θargmax P(θ∣D)
贝叶斯公式: P(θ∣D)=P(D)P(D∣θ)⋅P(θ)
原理:
- 消息传递:BP算法通过在因子图上的节点之间传递消息来进行推断。每个节点根据收到的消息更新自己的置信度,然后将更新后的消息传递给其相邻的节点,直到达到收敛或达到最大迭代次数为止
步骤:
- 初始化:初始化每个节点的信念值和消息
- 消息传递:在因子图上进行消息传递,直到收敛或达到最大迭代次数
- 计算结果:根据收敛后的节点信念值,计算边缘概率分布或进行最大后验概率估计
这段代码是用Python来计算在链式结构马尔可夫随机场上的最大积置信传播(Max-Product Belief Propagation)。下面我会逐步解释代码的功能:
Python示例:
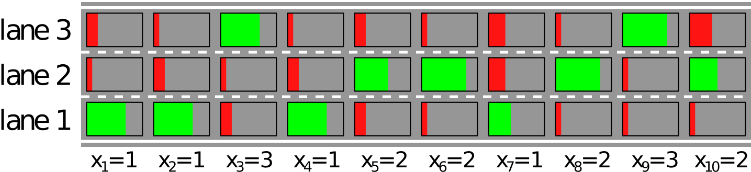
判断车辆最可能行驶的车道,由于有一些噪声导致了一些错误,初始值为 unary

定义马尔可夫随机场模型的参数:
# unary: Nx3 matrix 一元势函数f_i
unary = np.array([[0.7,0.1,0.2],[0.7,0.2,0.1],[0.2,0.1,0.7],[0.7,0.2,0.1],
[0.2,0.6,0.2],[0.1,0.8,0.1],[0.4,0.3,0.3],[0.1,0.8,0.1],
[0.1,0.1,0.8],[0.1,0.5,0.4]])
# pairwise: 3x3 matrix 二元势函数g(转移概率)
pairwise = np.array([[0.8,0.2,0.0],[0.2,0.6,0.2],[0.0,0.2,0.8]])一元势函数表示每个变量在各个状态下的初始概率,二元势函数表示变量之间的转移概率,如
pairwise[0][0]=0.8就表示在第一个车道变到第一车道(维持在当前车道)的概率为0.8
1 获取模型参数
[num_vars, num_states] = unary.shapeunary是一个二维数组,表示每个变量的一元势函数(unary potentials),其中每一行对应一个变量(某时刻在每个车道的概率),每一列对应一个状态(在哪个车道)num_vars表示变量的数量,即unary数组的行数num_states表示每个变量可能的状态数量,即unary数组的列数
2 计算消息
创建一个空的二维数组 msg,用于存储消息。数组的行数是 num_vars - 1,表示消息的数量,每一行对应一个变量。数组的列数是 num_states,表示每个消息可能的状态数量。
msg = np.zeros([num_vars - 1, num_states]) #一共9个消息(9个点与点的连接)3 消息传递
消息传递的核心是通过计算变量之间的乘积来更新消息,并选择这个乘积中的最大值作为传递的消息,从而选择最有可能的状态作为消息传递的结果。
for i in range(num_vars - 2, -1, -1):
if i == num_vars - 2:
msg[i] = np.max(pairwise * unary[i + 1, :], 1)
else:
msg[i] = np.max(pairwise * unary[i + 1, :] * msg[i + 1], 1)消息从后往前传递:
- 计算从倒数第二个变量到最后一个变量的消息:直接
unary乘上pairwise,并取乘积中的最大值 - 计算其他变量之间的消息:
unary、pairwise和前一个变量的消息的乘积,并取乘积中的最大值
4 计算边缘概率分布和MAP
创建一个空的二维数组
max_marginals,用于存储边缘概率。数组的行数是num_vars,表示变量的数量,每一行对应一个变量。数组的列数是num_states,表示每个变量可能的状态(一共3个车道)max_marginals = np.zeros([num_vars, num_states])创建一个大小为
num_vars的一维数组map,用于存储每一个变量的MAP(即对于每一个时刻,最可能选择的车道)map = np.zeros(num_vars, dtype=int)对于每个变量
i:- 第一个,则边缘概率就等于该变量的消息
msg[i, :] - 最后一个,则边缘概率等于前一个变量到当前变量的转移概率乘以当前变量的一元势函数
- 对于其他变量,边缘概率等于前一个变量到当前变量的转移概率乘以当前变量的一元势函数乘以当前变量的消息
for i in range(num_vars): if i == 0: max_marginals[i, :] = msg[i, :] if i == num_vars - 1: max_marginals[i, :] = pairwise[map[i - 1], :] * unary[i, :] else: max_marginals[i, :] = pairwise[map[i - 1], :] * unary[i, :] * msg[i, :] map[i] = np.argmax(max_marginals[i, :])pairwise[map[i - 1], :]代表前一个时刻最可能在的车道所对应的转到各个车道的概率- 第一个,则边缘概率就等于该变量的消息
输出MAP估计值:
输出MAP估计值,即对每个变量边缘概率最大的所对应的状态(每个时刻最可能的车道)
print(map)
4 图像去噪
一元因子:
一元因子是关于单个像素的因子,它根据观察到的像素值来影响像素的状态。一个黑白图像,每个像素的状态只能黑色(0)或白色(1)
一元因子表示:以字典的形式表示,其中包含变量索引列表(vars)和值列表(vals)
vars:变量索引列表仅包含当前像素的索引索引计算 v×w+u 就是将像素的二维坐标 (u,v) 转换为一维索引,以便在因子图中进行处理和存储
vals:值列表包含两个值,分别表示像素为0、1的概率例如,如果观察到的像素值是0,则一元因子的值列表将为
1,0;如果观察到的像素值是1,则值列表将为0,1
成对因子:
成对因子是关于相邻像素之间关系的因子。我们希望相邻像素之间的状态越相似越好,这样图像看起来就更平滑了。
成对因子表示,如果两个相邻像素的状态相同,那么这种状态就更有可能发生,而如果状态不同,则可能性较低。
能量矩阵:一个 2×2 的单位矩阵
这意味着如果两个相邻像素的状态相同,它们之间的能量是
1如果它们的状态不同,能量是
0
这种设置使得相邻像素倾向于保持相同的状态,以实现图像的平滑
alpha:这个参数用来调节相邻像素之间的关系对能量的影响- 较大的
alpha值会增加相邻像素之间的相似性,从而产生更加平滑的图像,但过大会导致过度平滑化:失去细节、模糊和混淆 - 较小的
alpha值则会减弱相邻像素之间的关系,可能导致图像保留更多的细节信息,但也更容易受到噪声的影响
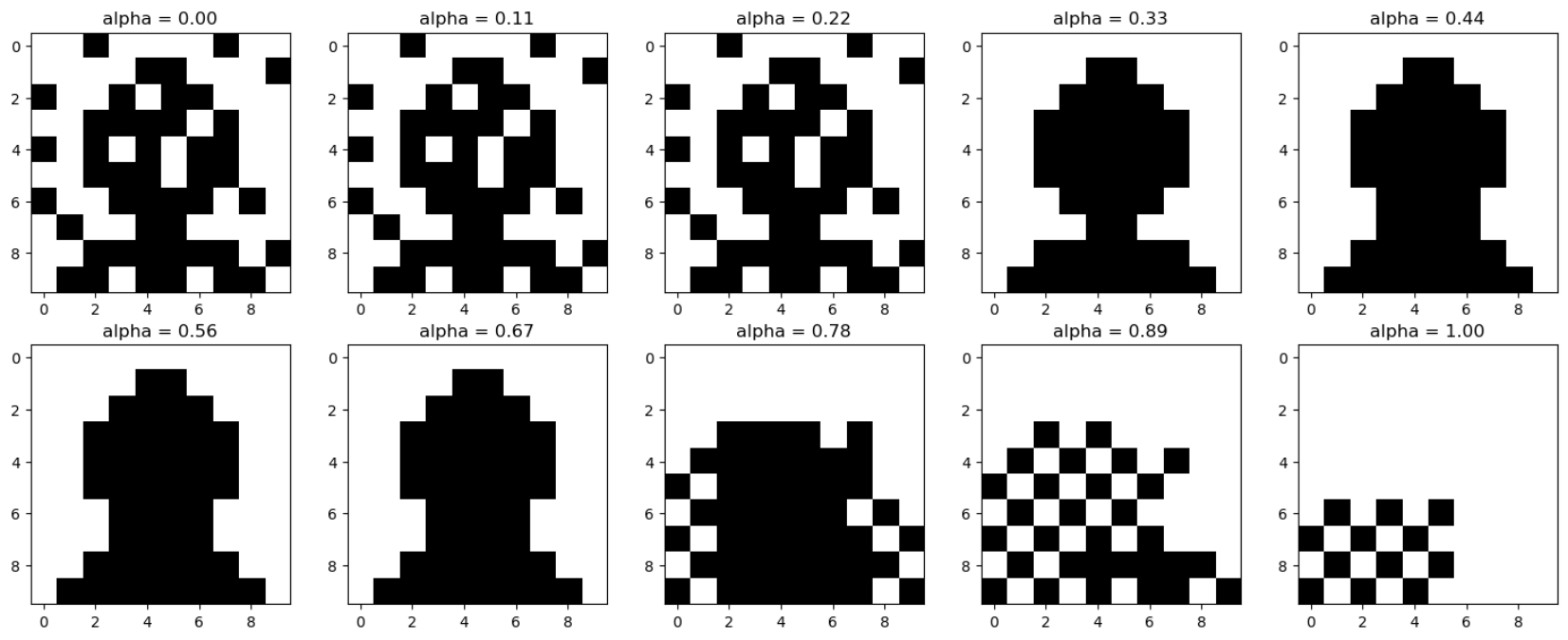
- 较大的