1 Overall

1.1 Task

World-Grounded Human Motion Recovery (HMR)：从单目视频中恢复世界坐标系下的人体动作，核心挑战在于世界坐标系的定义存在歧义，这在不同的视频序列之间可能会有所不同。

1.2 Old Method

通常是从相机视角中恢复人体的运动，但转换到世界坐标系时，常常无法保证重力方向对齐，且容易累积误差。例如，最近的 WHAM 方法通过自回归的方式预测全局姿势，但依赖于好的初始化，并且在长时间序列中可能出现错误积累。

自回归模型描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测

1.3 GVHMR

GV坐标系统：该系统天然对齐重力方向，并且每一帧的定义都是唯一的，因此能够有效减少学习图像与姿势映射时的歧义。

估计出的姿势可以通过相机的旋转矩阵转换回世界坐标系，从而形成一个全局的运动序列。此外，每一帧的独立估计方法避免了自回归方法中可能出现的误差积累问题。

Contributions：

1. GV坐标系统：通过这个新坐标系统来估计重力感知的人体姿势，避免了重力方向上的误差积累。
2. 基于 Transformer：通过旋转位置编码（RoPE），能够有效处理长时间序列，并提高运动估计的精度。并且模型引入了一个掩码来限制每一帧的感受野，从而避免了复杂的滑动窗口操作，实现了对任意长序列的并行推理。
3. 还为双手和双脚预测了静止标签，用来修正脚滑动和全局轨迹，从而提升结果的准确性。

2 Related Work

2.1 相机空间人体动作恢复

许多现代3D人体动作恢复方法都基于参数化人体模型（SMPL）。目标是通过给定一张图像或视频，将人体模型与图像中的2D信息对齐。

• 早期方法：早期的方法采用基于优化的方式，通过最小化重投影误差来实现模型与图像的对齐。
• 回归方法：近年来，许多基于回归的方法被提出，通过大规模数据集训练，直接从输入的图像中预测 SMPL 模型的参数。这些方法比早期的优化方法更为高效，且可以通过深度学习提高精度。
• 结构设计和相机参数：一些研究提出了专门的网络结构，或者通过加入相机参数来提高准确性。
• 时序信息的利用：为了利用时间序列信息，提出直接从视频中预测人体骨架的动作序列。
• 模型改进：在恢复人体网格方面，许多方法建立在 HMR 框架上，使用卷积神经网络（CNN）、递归神经网络（RNN）或 Transformer 等模型来提取时序信息。

这些方法得到的结果通常是在相机坐标系下。相机坐标系会随着相机的运动而变化，因此当相机移动时，人体的运动可能会变得不符合物理规律。例如，人体的姿势可能会因相机的滚动（roll）和俯仰（pitch）等运动而出现倾斜，导致恢复的人体运动不准确。

2.2 世界坐标系下的人体动作恢复

为了在重力感知的世界坐标系下恢复人体运动，传统方法通常需要额外的地面平面标定或重力传感器。例如，使用多相机系统时，通过在地面上放置标定板来重建地面平面和全局尺度；而使用IMU（惯性测量单元）的方法通过陀螺仪和加速度计估计重力方向。

• 多相机系统：在多相机捕捉系统中，通过地面标定来重建地面平面和全局尺度。
• IMU 方法：IMU（惯性测量单元）基于陀螺仪和加速度计来估计重力方向，并将人体动作投影到重力方向上。
• 从单目视频恢复全局运动：一些研究致力于通过单目视频来估计全局人体运动。例如，通过物理规律重建人体运动，但需要提供场景信息；或者尝试从人体的运动线索预测全局轨迹。尽管这些方法有所改进，但由于相机和人体运动是耦合的，它们的结果往往会产生噪声。
• SLAM 与预学习人体运动先验：方法如 SLAHMR 和 PACE 将 SLAM 与预先学习的人体运动先验结合，在优化框架中进行计算。这些方法尽管有很好的表现，但优化过程通常非常耗时，并且在长时间视频序列中可能存在收敛问题。此外，这些方法通常无法获得与重力对齐的全局人体运动。

2.3 前沿工作

• WHAM 是目前最相关的工作之一。它通过自回归方式逐帧回归姿势和位移，尽管它取得了一定的成功，但依赖于良好的初始化，并且在长时间序列中会因误差积累而导致性能下降。
• WHAC 通过视觉里程计（visual odometry）将相机坐标系下的结果转换到世界坐标系，并依赖另一个网络来修正全局轨迹。
• TRAM 利用 SLAM 技术恢复相机运动，并通过场景背景推导运动的尺度，也将相机坐标系下的结果转换为世界坐标系下的运动。

与这些方法相比，GVHMR 有几个显著的优势：

• 它不需要额外的修正网络，能够直接从单目视频中预测与世界重力对齐的全局人体运动。
• 本方法通过引入重力视图坐标系（GV），有效减少了相机运动和人体运动耦合带来的噪声，并且不依赖于复杂的优化过程。

3 Method

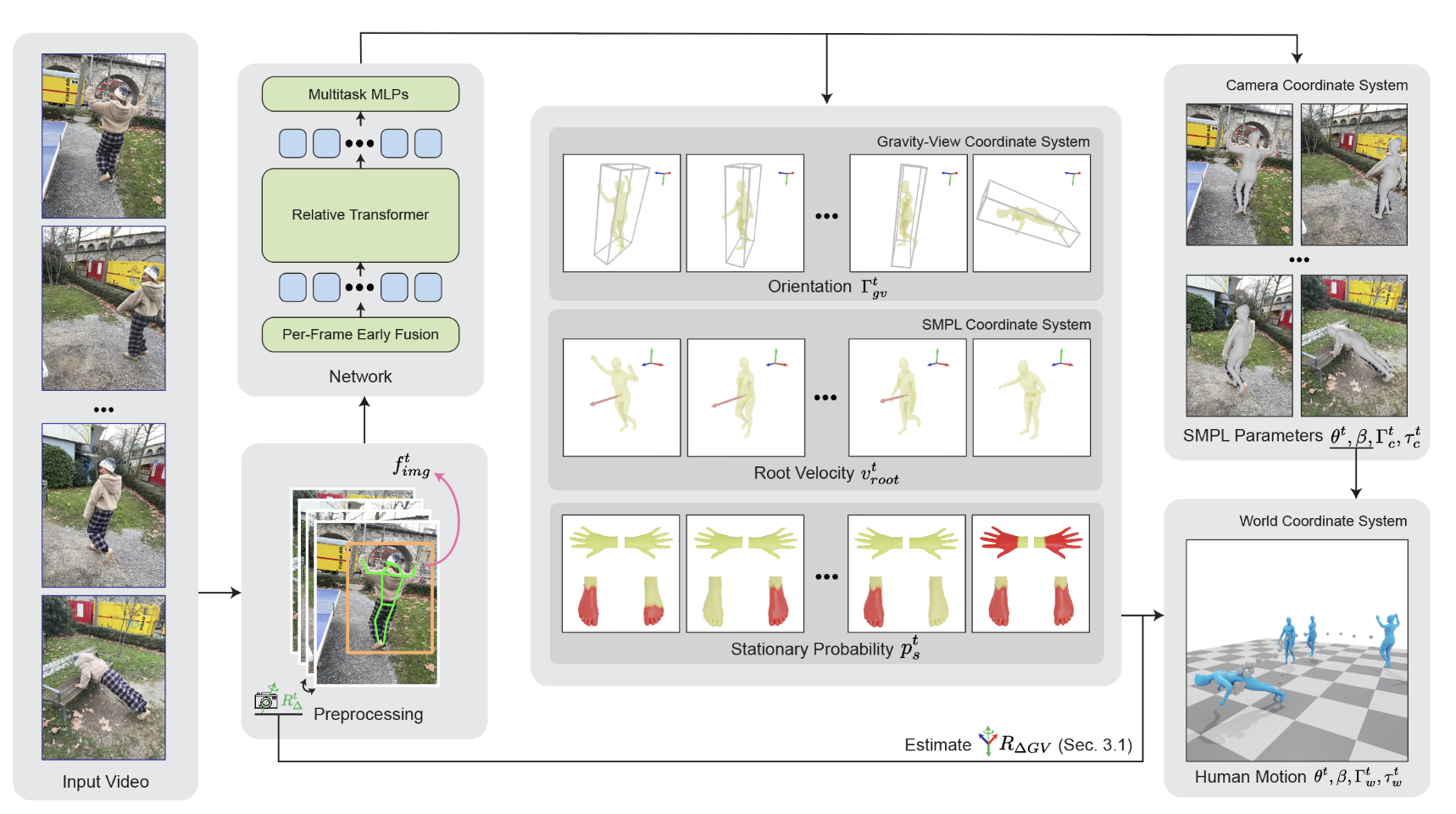
给定单目视频序列 $\{I^t\}_{t=0}^T$，GVHMR 的目标是预测以下三部分内容：

1. 局部身体姿态与形状参数：

   • 局部姿态：$\{\theta^t \in \mathbb{R}^{21 \times 3}\}_{t=0}^T$，表示 SMPL-X 模型中 21 个关节的旋转参数（每个关节 3 个自由度）。
   • 形状系数：$\beta \in \mathbb{R}^{10}$， SMPL-X 模型中控制人体体型（如身高、胖瘦）。

2. 从 SMPL 空间到相机空间的轨迹：

   • 朝向：$\{\Gamma_c^t \in \mathbb{R}^3\}_{t=0}^T$，表示人体在相机坐标系下的旋转（如欧拉角或轴角表示）。
   • 平移：$\{\tau_c^t \in \mathbb{R}^3\}_{t=0}^T$，表示人体在相机坐标系下的位置偏移。

3. 从相机空间到世界空间的轨迹：

   • 朝向：$\{\Gamma_w^t \in \mathbb{R}^3\}_{t=0}^T$，表示人体在重力对齐的世界坐标系下的旋转。
   • 平移：$\{\tau_w^t \in \mathbb{R}^3\}_{t=0}^T$，表示人体在世界坐标系下的全局位置。

3.1 全局轨迹表示（Global Trajectory Representation）

目标：解决旋转模糊问题 rotation ambiguity

因为在建立世界坐标系时，旋转轴（如x轴和z轴）相对于已知的重力方向y轴无法唯一确定，这样就导致了旋转不确定性。而通过定义重力视图坐标系（GV坐标系），可以通过约束相机视角和重力方向的关系来解决这一问题。

引入 Gravity-View (GV) 坐标系，其定义基于两个方向：

1. 重力方向（Y 轴）：由物理约束或传感器数据确定。
2. 相机视图方向（Z 轴）：垂直于图像平面。

GV 坐标系的构建步骤：

1. Y 轴：对齐重力方向 $\vec{g}$

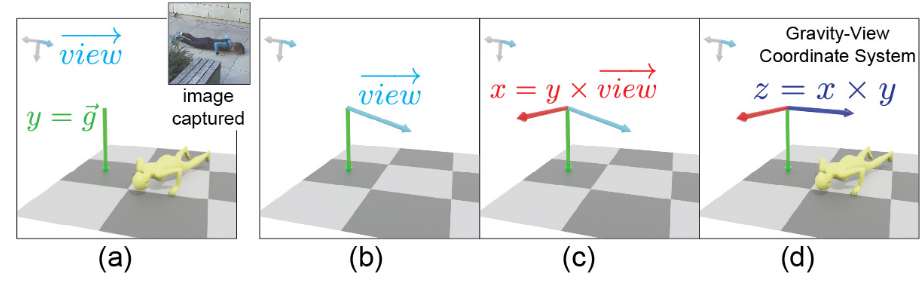
2. X 轴：通过叉乘 $\vec{g} \times \vec{view}$ 确定（坐标系需要相互垂直）

   如果多个相机的视角方向 $\vec{view}$ 在 YZ 平面内变化，但叉乘结果 $\vec{g} \times \vec{view}$ 的方向相同（仅大小不同），则这些相机会对应同一个 GV 坐标系。这种情况下，GV 坐标系的唯一性无法保证，可能对全局轨迹恢复产生影响？

3. Z 轴：通过右手定则计算 $\vec{z} = \vec{x} \times \vec{y}$

全局轨迹恢复：

将每帧独立预测的 GV 坐标系下的人体朝向（$\Gamma_{GV}^t$）转换为一个全局一致的世界坐标系（$W$）下的轨迹（$\Gamma_w^t, \tau_w^t$），确保重力方向对齐且误差不累积。

GV 坐标系为每帧提供唯一且重力对齐的参考系。通过将每帧的 $GV_t$ 坐标系对齐到初始帧 $GV_0$ （作为世界参考系 $W$ ），可恢复全局一致的轨迹。

全局轨迹恢复流程：

1. 静态相机：所有帧的 GV 坐标系相同

   1. 全局朝向：$\Gamma_w^t = \Gamma_{GV}^t$（直接使用 GV 坐标系下的预测结果）。

   2. 全局平移：

      $$\tau_t^w = \begin{cases} [0, 0, 0]^T, & t = 0 \\ \sum_{i=0}^{t-1} \Gamma_w^i v^i_{root}, & t > 0 \end{cases}$$

      • 预测每帧的根节点速度 $v_{\text{root}}^t$（SMPL 坐标系下的局部位移）
      • 将速度转换到世界坐标系：$v_{\text{world}}^t = \Gamma_w^t \cdot v_{\text{root}}^t$
      • 累积速度得到全局平移： $\tau_w^t = \sum_{i=0}^{t-1} v_{\text{world}}^i$

2. 动态相机：利用相邻帧的相机相对旋转 $R_\Delta^t$，计算 GV 坐标系的相对旋转 $R_{\Delta GV}^t$，将所有帧对齐到 $GV_0$（世界坐标系）。

   1. 计算 GV 坐标系间的相对旋转 $R_{\Delta GV}^t$ ：输入相邻帧的相机相对旋转 $R_\Delta^t$（VO 或陀螺仪估计）

      • 计算相机坐标系到 GV 坐标系的旋转矩阵： $R_{c2gv}^t = \Gamma_{GV}^t \cdot (\Gamma_c^t)^{-1}$

      • 将相机视图方向转换到 GV 坐标系： $\vec{view}_{GV}^t = R_{c2gv}^t \cdot \vec{view}_{c}^t$

      • 利用相机相对旋转 $R_\Delta^t$，将 $\vec{view}_{GV}^t$ 转换到前一帧的坐标系： $\vec{view}_{GV}^{t-1} = (R_\Delta^t)^{-1} \cdot \vec{view}_{GV}^t$

      • 投影到 xz 平面，计算两视图方向的夹角 $\theta$，构造绕 y 轴的旋转矩阵 $R_{\Delta GV}^t$ （其只围绕着y轴进行旋转）

        

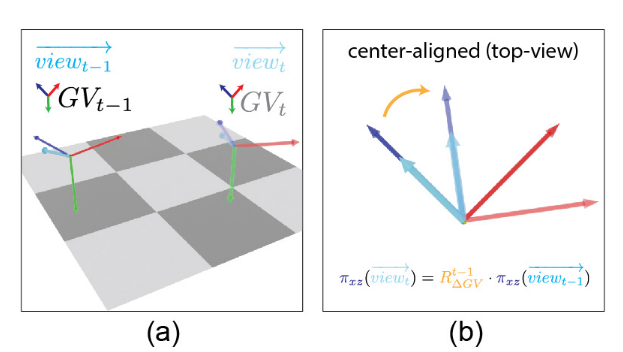
   2. 全局朝向：将每帧的 $\Gamma_{GV}^t$ 通过累积相对旋转 $R_{\Delta GV}^t$ 对齐到 $GV_0$： $\Gamma_w^t = \prod_{i=1}^t R_{\Delta GV}^i \cdot \Gamma_{GV}^t$

   3. 全局平移：与静态相机相同，但使用对齐后的 $\Gamma_w^t$ 转换速度： $\tau_w^t = \sum_{i=0}^{t-1} \Gamma_w^i \cdot v_{\text{root}}^i$

总结优点：

• 模型仅需预测相对GV坐标系的简单旋转，无需处理复杂的世界坐标系模糊性
• 非自回归预测：每帧的 $\Gamma_{GV}^t$ 独立预测，无需依赖前一帧结果，避免误差累积，且支持长序列实时处理。
• 即使相机相对旋转存在误差（如使用视觉里程计 DPVO 而非真实陀螺仪 GT Gyro），GV 的Y轴约束仍能保证重力方向一致性。

3.2 网络设计

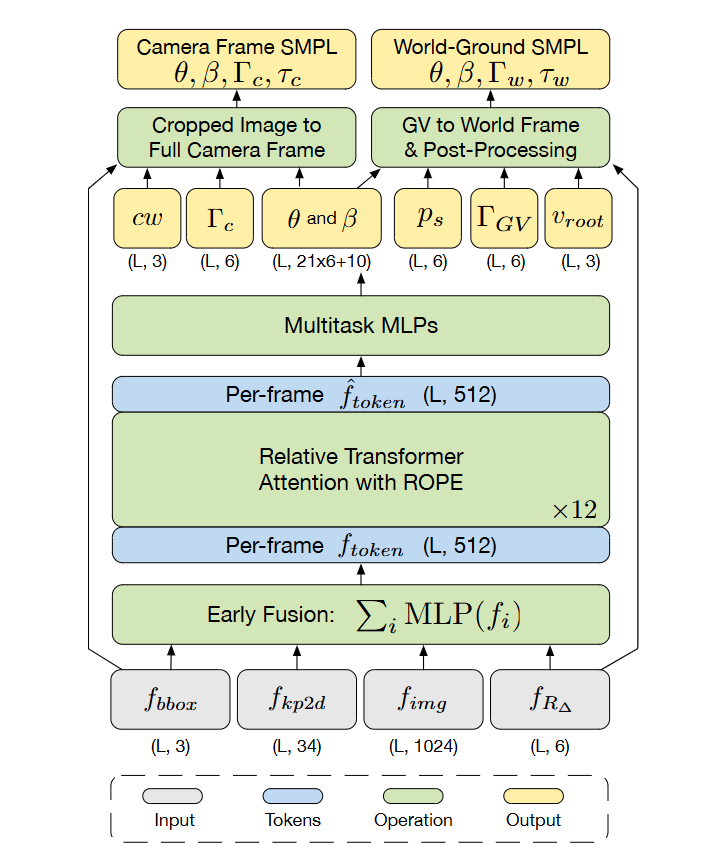
(1) 输入预处理与特征提取

GVHMR 的输入为单目视频序列，进行预处理得到四种特征表示：

• 边界框（Bounding Boxes）： 使用 YOLOv8 或类似检测模型实时跟踪人体区域，提供每帧中人体的位置和尺度信息。
• 2D 关键点（2D Keypoints）： 基于 ViTPose 等姿态估计模型，提取人体 2D 关节坐标，提供局部姿态的强监督信号。
• 图像特征（Image Features）： 通过 ViT（如 HMR2.0 的 ViT 编码器）提取全局语义特征，捕捉外观和上下文信息。
• 相对相机旋转（Relative Camera Rotations）： 利用视觉里程计（如 DPVO）或陀螺仪数据，估计相邻帧间的相机相对旋转矩阵 $R_\Delta^t$ ，用于跨帧对齐。

(2) 早期特征融合 Early-Fusion

将异构特征统一为紧凑的时序 token

1. 独立映射：四类特征分别通过独立的 MLP 映射到 512 维空间。

   • 边界框 → MLP → $\mathbf{f}_{\text{bbox}}^t \in \mathbb{R}^{512}$
   • 2D 关键点 → MLP → $\mathbf{f}_{\text{key}}^t \in \mathbb{R}^{512}$
   • 图像特征 → MLP → $\mathbf{f}_{\text{img}}^t \in \mathbb{R}^{512}$
   • 相对相机旋转 → MLP → $\mathbf{f}_{\text{cam}}^t \in \mathbb{R}^{512}$

2. 逐元素相加：生成每帧的融合 token

   $$\mathbf{f}_{\text{token}}^t = \mathbf{f}_{\text{bbox}}^t + \mathbf{f}_{\text{key}}^t + \mathbf{f}_{\text{img}}^t + \mathbf{f}_{\text{cam}}^t$$

   加法融合保留各模态信息，避免拼接（concatenation）导致的维度爆炸。实验表明，加法融合在计算效率和性能间取得平衡。

(3) Relative Transformer

它通过相对位置编码和注意力掩码的机制，使模型能够更好地理解和利用序列中 token 之间的相对位置关系，而不是仅仅依赖绝对位置信息。这种方法在处理长序列和需要关注局部上下文的任务中表现出色，例如人体运动恢复，其中相邻帧之间的相对运动比绝对位置更重要。

1. Rotary Positional Embedding (RoPE)：通过旋转矩阵将相对位置信息编码到注意力机制中。

   人类运动的绝对位置是不明确的（例如，运动序列的开始可以是任意的）。相比之下，相对位置是明确定义的并且可以容易地学习。

   • 公式：

     $$a^{ts} = (\mathbf{W}_q \mathbf{f}_{\text{token}}^t)^\top \mathbf{R}(\text p^s-\text p^t) (\mathbf{W}_k \mathbf{f}_{\text{token}}^s)$$

     其中 $\mathbf{R}(\cdot)$ 为旋转矩阵，将 Query 和 Key 向量按相对位置 $s-t$ 旋转。

   • 实现：

     • 每帧的融合 token $\mathbf{f}_{\text{token}}^t \in \mathbb{R}^{512}$ 进入 Transformer 层
     • 在自注意力层中，应用 RoPE 编码相对位置

   • 作用：

     • 显式建模相对位置关系，提升长序列建模能力。
     • 支持序列长度外推，无需重新训练。

2. 注意力掩码：

   • 设计：限制每帧 token 仅关注前后 $L$ 帧（如 $L=120$），即：

     $$m^{ts} = \begin{cases} 0, & \text{if } |t-s| \leq L \\ -\infty, & \text{otherwise} \end{cases}$$

   • 作用：

     • 减少计算复杂度，支持无限长视频推理。
     • 强制模型关注局部时序上下文，避免无关帧干扰。

引入旋转位置嵌入和注意力掩码，为 token 注入相对特征，第 $t$ 个 token 通过 Transformer 层后的输出：

$$o_t = \sum_{i \in T} \underset{s \in T}{\text{Softmax}} \left( a^{ts} + m^{ts} \right) W_v f^i_{token}$$

(4) 网络输出

将 relative transformer 输出的新的 $\mathbf{f}_{\text{token}}^\prime$ 输入 multitask MLPs，得到：

1. 相机空间参数

   • 弱透视相机参数 $cw$ ：弱透视模型假设物体深度远小于到相机的距离，简化投影为缩放和平移（2D 位移 + 缩放因子）。

2. 人体姿态与形状参数

   • 局部姿态 $\theta \in \mathbb{R}^{21 \times 3}$ ：SMPL-X 模型的 21 个关节旋转参数（轴角表示）

   • 形状系数 $\beta \in \mathbb{R}^{10}$ ：控制体型特征（身高、肩宽、胖瘦等）

3. 全局运动参数

   • 相机坐标系朝向 $\Gamma_c$：人体相对于相机坐标系的旋转

   • GV 坐标系朝向 $\Gamma_{GV}$ ：人体在 GV 坐标系下的旋转

   • 根节点速度 $v_{\text{root}}$ ：SMPL 坐标系下根节点的位移速度

4. 静止标签 $p_j$ ：预测手、脚趾、脚跟等关节的静止概率，标识关节是否在特定帧处于静止状态。在后处理中用于抑制非物理运动（如脚部滑动）。

(5) 后处理优化

后处理目标是将网络输出的粗糙运动优化为平滑、物理合理的结果，具体步骤如下：

1. 全局平移修正：若某关节（如脚部）的静止概率 $p_j > 0.5$，则强制其在世界坐标系中的位置固定
2. 逆运动学（IK）优化：使用CCD算法，根据修正后的全局平移，反推局部关节旋转 $\theta$，消除足部滑动等异常。
3. 运动平滑处理：约束加速度和关节运动连续性，减少抖动。

(6) Loss

• MSE 损失：除静止概率外的所有回归任务，如姿态、形状、速度等连续变量。
• BCE 损失：用于静止标签分类。
• L2 损失：约束 3D 关节、顶点、平移等物理合理性。

3.3 实现细节

1. 网络架构

   • Transformer：

     • 层数：12 层。
     • 注意力头数：每层 8 头
     • 隐藏层维度：512

   • MLP：两层线性层，中间使用 GELU 激活函数

2. 训练数据集：GVHMR 在以下混合数据集上从头训练：AMASS、BEDLAM、H36M、3DPW

3. 数据增强

   • 2D 关键点增强：遵循 WHAM 的方法，对 2D 关键点进行随机扰动（如平移、缩放、旋转），模拟不同视角和尺度变化。

   • 相机轨迹模拟：对 AMASS 数据，生成静态和动态相机轨迹。

   • 边界框生成：基于 2D 关键点生成人体边界框，用于归一化和特征提取。

4. 图像特征提取

   • 视频数据集（如 H36M、3DPW）：使用固定编码器（如 HMR2.0 的 ViT）提取图像特征，捕捉全局语义信息。

   • 非视频数据集（如 AMASS）：图像特征置零，仅依赖 2D 关键点和边界框信息。

5. 训练参数

   • 序列长度：(L = 120) 帧（约 4 秒，30 FPS）

   • 批量大小：256

   • 训练轮数：500 轮

   • 硬件配置：2 块 RTX 4090 GPU，训练耗时约 13 小时