1 视差图

视差图：以左视图视差图为例，在像素位置p的视差值等于该像素在右图上的匹配点的列坐标减去其在左图上的列坐标

视差图和深度图：

$$z = \frac{fb}{d}$$

其中 $d$ 是视差， $f$ 是焦距， $b$ 是基线长度

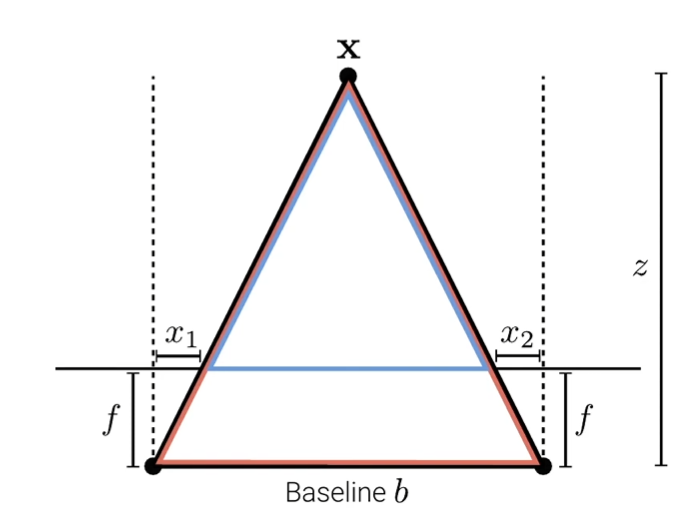
所以，视差越大 ——> 深度越小

2 传统方法

原理：是在给定窗口大小的情况下，对左图像和右图像的对应窗口进行比较，计算它们之间的绝对差的总和，从而确定最佳匹配的视差

SAD：Sum of Absolute Differences 即差的绝对值和

$$SAD(x,y,d) = |w_L(x, y) - w_R(x-d, y)|$$

大致流程：

1. 对左图像和右图像分别进行零填充以适应窗口的边界

   为在计算这些像素的视差时，窗口可能会超出图像的范围

2. 对于左图像的每个像素，依次遍历整个图像

3. 对于每个像素，以其为中心取窗口大小的区域，并在右图像中搜索匹配窗口

   # 一定是减去d，因为右边图像是左边图像向右平移d个像素
   window_right = image_right[y:y + window_size, x - d:x - d + window_size]

   设置一个 max_disparity 来限制搜索范围

4. 计算左图像窗口和右图像匹配窗口的绝对差的总和，即SAD值

   now_sad = np.sum(np.abs(window_left - window_right))

5. 找到最小的SAD值，将对应的视差 d 保存到该像素位置

代码实现：

def sad(image_left, image_right, window_size=3, max_disparity=50):
    D = np.zeros_like(image_left)
    height = image_left.shape[0]
    width = image_left.shape[1]
    # 零填充
    padding = window_size // 2
    image_left = add_padding(image_left, padding).astype(np.float32)
    image_right = add_padding(image_right, padding).astype(np.float32)

    for y in range(height):
        for x in range(width):
            # 左边图像的窗口
            window_left = image_left[y:y + window_size, x:x + window_size]
            best_disparity = 0
            min_sad = float('inf')
            for d in range(max_disparity):
                if x - d < 0:
                    continue
                # 一定是减去d，因为右边图像是左边图像向右平移d个像素
                window_right = image_right[y:y + window_size, x - d:x - d + window_size]
                now_sad = np.sum(np.abs(window_left - window_right))

                if now_sad < min_sad:
                    min_sad = now_sad
                    best_disparity = d

            # 保存SAD
            D[y, x] = best_disparity

    return D # 返回视差图

3 卷积方法

传统方法很慢，卷积方法避免了的嵌套循环，效率比起传统方法高了很多

利用图像卷积的思想，通过对每个候选视差值计算绝对差图像，并将其与一个均值滤波器进行卷积操作来实现视差图的计算

具体步骤如下：

1. 对于每个候选的视差值，计算两幅图像在水平方向上的绝对差

   img_diff = np.abs(image_left - right_shifted)

2. 将计算得到的绝对差图像与一个均值滤波器进行卷积操作。均值滤波器的大小应与窗口大小相匹配，用于平滑绝对差图像，从而减少噪声和不稳定性

   # 平滑均值滤波卷积核
   kernel = np.ones((window_size, window_size)) / (window_size ** 2)
   # 通过卷积运算，可以计算出每个像素邻域的总差异，也就是SAD值
   img_sad = convolve(img_diff, kernel, mode='same')

   卷积的作用：

   1. 平滑处理：卷积可以用来对图像进行平滑处理，也就是降噪。当卷积核是一个均值滤波器，就可以用于计算图像中每个像素的邻域的平均值。这样可以减少图像中的随机噪声，使图像变得更加平滑
   2. 计算局部差异：在计算左图和右图之间的 SAD 值时，需要对每个像素的邻域进行操作。这可以通过卷积来实现。卷积结果中的每个像素值表示了对应的像素邻域在左图和右图之间的差异程度

3. 对于每个像素，选择具有最小卷积结果的视差值作为最终的视差值

代码实现：

def sad_convolve(image_left, image_right, window_size=3, max_disparity=50):
    # 零填充
    padding = window_size // 2
    image_left = add_padding(image_left, padding).astype(np.float32)
    image_right = add_padding(image_right, padding).astype(np.float32)
    SAD = np.zeros((image_left.shape[0], image_left.shape[1], max_disparity + 1))
	# 卷积核
    kernel = np.ones((window_size, window_size)) / (window_size ** 2)
	# 范围很重要，要覆盖0和max_disparity才行
    for d in range(0, max_disparity才行 + 1):
        if d == 0:
            right_shifted = image_right
        else:
            right_shifted = np.zeros_like(image_right)
            right_shifted[:, d:] = image_right[:, :-d]

        img_diff = np.abs(image_left - right_shifted)
        # 通过卷积运算，可以计算出每个像素邻域的总差异，也就是SAD值
        img_sad = convolve(img_diff, kernel, mode='same')
        SAD[:, :, d] = img_sad

    D = np.argmin(SAD, axis=2) # 选出算出最小SAD的视差值
    return D

4 问题

块匹配方法在处理时存在一些限制，主要包括以下几点：

1. 局部窗口匹配：块匹配方法通常只考虑局部窗口内的像素信息进行匹配，而对于同质区域，局部窗口内的像素可能非常相似，导致匹配困难

2. 窗口大小选择：选择合适的窗口大小对于块匹配的性能至关重要。

   • 小窗口：在纹理丰富的区域，可以选择较小的窗口；但对于同质区域可能无法捕捉到同质区域的整体特征
   • 大窗口：在纹理稀疏的区域，应选择较大的窗口大小；但可能会将不同物体的特征混合在一起，导致误匹配，但较大的窗口大小会增加计算量

   窗口大小	结果
   3
   7
   15

5 Siamese神经网络

Siamese神经网络由两个相同的子网络组成，这两个子网络共享相同的参数（权重和偏置）。无论输入是什么，它们都会通过相同的网络结构进行处理

1. 特征提取：给定两个输入，它们分别通过两个子网络进行前向传播，从而得到它们的特征表示。这些特征表示捕捉了输入的关键信息
2. 相似性评估：得到特征表示后，Siamese神经网络通过某种方式比较这两个特征表示，以确定它们之间的相似性。我们使用余弦相似度来操作

其有两种结构：

1. 余弦相似度 (Cosine Similarity)：

   
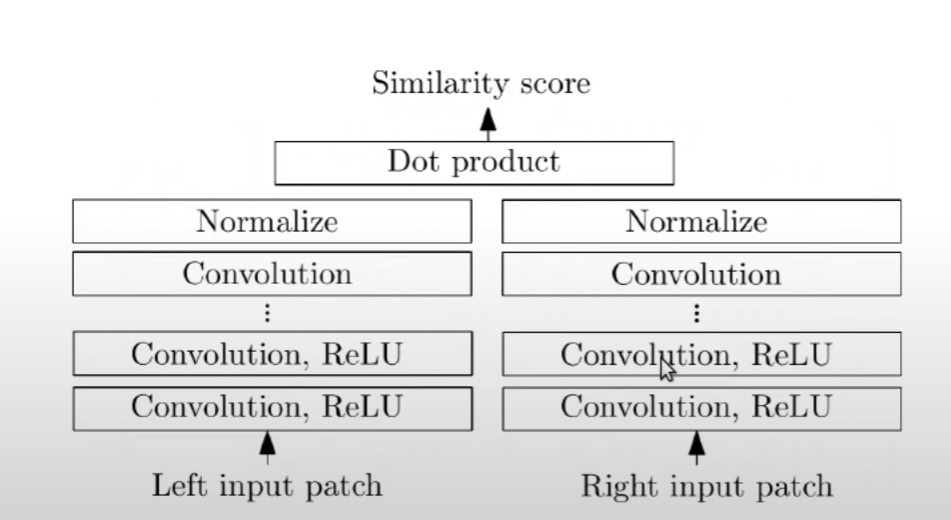
   • 原理：计算两个特征向量之间的夹角余弦值，范围在-1到1之间。值越接近1，表示两个向量越相似；值越接近-1，表示两个向量越不相似；值接近0表示两个向量之间没有线性关系
   • 应用：通过计算特征向量之间的余弦相似度，可以衡量它们在特征空间中的方向是否相似，其没有MLP，卷积层后直接标准化进行点乘，速度非常快，且效果也较好

2. 学习相似性 (Learned Similarity)：

   
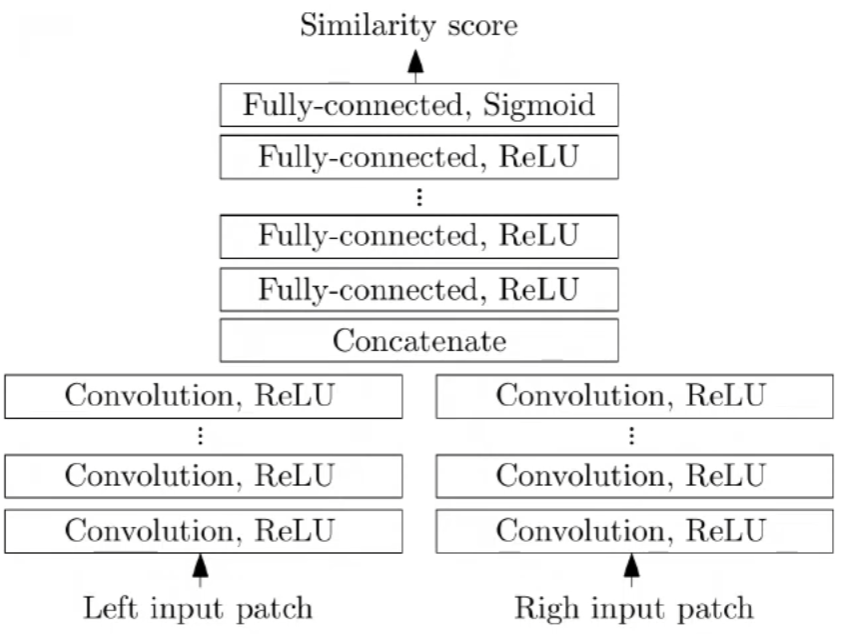
   • 原理：需要训练一个神经网络，该网络将输入的特征向量映射到一个标量值，表示它们之间的相似性得分
   • 应用：神经网络可以学习到更复杂的特征表示，并且可以捕捉输入之间的非线性关系。但是，由于MLP的计算成本较高，会较于前者较慢