详细解析Barlow Twins：自监督学习中的创新方法

1442字约5分钟

3DVision

2024-05-30

首先先简单了解一下机器学习中，主要有三种学习范式：监督学习、无监督学习和自监督学习：

监督学习：依赖带标签的数据，通过输入输出映射关系进行训练。
无监督学习：不依赖标签，关注数据的内在结构和模式。
自监督学习：利用数据本身生成标签，通过预训练任务学习有效的特征表示。

Barlow Twins

Barlow Twins是一种基于信息论的自监督学习方法，其目标是减少神经元之间的冗余。该方法要求神经元对数据增强具有不变性，但彼此独立。

在实际训练中，通过反向传播（backpropagation）调整神经网络的参数，使得交叉相关矩阵的对角线元素尽可能大，而非对角线元素尽可能小——接近单位矩阵，从而达到上述目标。

1 例子

假设我们有一张图片 $X$ ，经过两个不同的数据增强得到图像 $Y^A$ 和 $Y^B$ ，其再通过相同的神经网络得到特征表示 $Z^A$ 和 $Z^B$ （假设有RGB三维）。由于是同一张图片， $Z^A$ 的蓝色与 $Z^B$ 的蓝色应该相似（红绿同理），同时为了最大限度减少冗余，我们希望特征彼此本身不同（即 $Z^A$ 中的蓝绿红彼此不同） —— 对数据增强保持不变，但独立于其他。

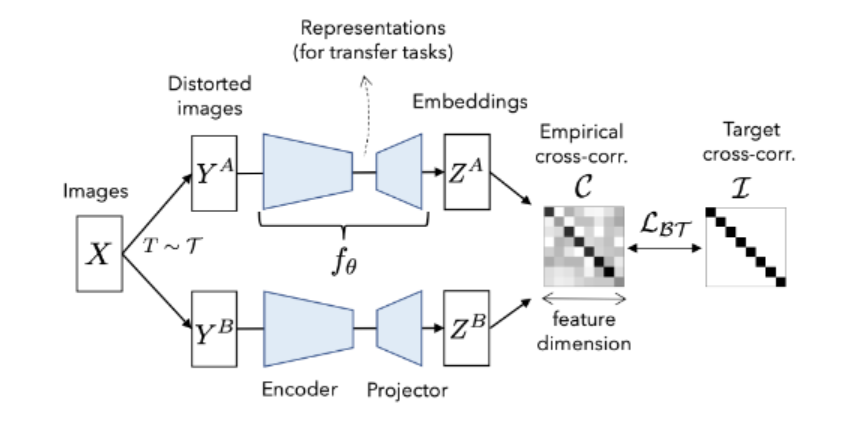
数学上描述即为：计算特征表示 $Z^A$ 和 $Z^B$ 的交叉相关矩阵，目标为使该矩阵接近单位矩阵。

这张图展示了Barlow Twins方法的主要流程。具体步骤如下：

数据增强：
- 从输入图像 $X$ 出发，使用不同的数据增强变换 $T$ 生成两组扭曲图像 $Y^A$ 和 $Y^B$ 。这些变换包括随机裁剪、翻转、颜色抖动等。
特征提取：
- 将扭曲图像 $Y^A$ 和 $Y^B$ 输入相同的神经网络 $f_\theta$ ，生成对应的特征表示 $Z^A$ 和 $Z^B$ 。
计算交叉相关矩阵：
- 计算特征表示 $Z^A$ $Z^{A}$ 和 $Z^B$ $Z^{B}$ 的交叉相关矩阵。目标是使该矩阵接近单位矩阵，从而：
  - 对角线元素：希望在不同数据增强下，相同神经元的特征表示具有高度相关性（接近1）。
  - 非对角线元素：希望不同神经元之间没有冗余（接近0）。

2 Loss计算

交叉相关矩阵 $C_{ij}$ 的计算

衡量了不同增强视图下神经元之间的相关性

C_{ij} = \frac{\sum_b z^A_{b,i} z^B_{b,j}}{\sqrt{\sum_b (z^A_{b,i})^2} \sqrt{\sum_b (z^B_{b,j})^2}}

$z^A_{b,i}$ 和 $z^B_{b,j}$ 分别表示第 $b$ 个样本在增强视图 $A$ 和 $B$ 中第 $i$ 和第 $j$ 个神经元的特征表示。

损失函数 $\mathcal{L}_{BT}$ ：

\mathcal{L}_{BT} = \sum_i (1 - C_{ii})^2 + \lambda \sum_i \sum_{j \neq i} C_{ij}^2

不变性项： $\sum_i (1 - C_{ii})^2$ 这个部分希望对角线上的元素 $C_{ii}$ 尽可能接近1，表示在不同增强视图下，相同神经元的特征表示高度相关。
冗余减少项： $\lambda \sum_i \sum_{j \neq i} C_{ij}^2$ 这个部分希望非对角线上的元素 $C_{ij}$ 尽可能接近0，表示不同神经元之间没有冗余。系数 $\lambda$ 是一个超参数，用来平衡这两个项的权重。

整个Barlow Twins的关键即损失函数：

返回方阵非对角线元素的扁平（一维）视图函数：

x.flatten()[:-1]：首先，将方阵x扁平化（即将其转换为一维数组），然后删除最后一个元素。扁平化后的数组中，最后一个元素是方阵的最后一个对角线元素。
.view(n - 1, m + 1)：然后，将扁平化后的数组重新塑形为一个(n - 1, m + 1)的矩阵。这个矩阵的每一行都包含了原方阵的一行元素。
[:, 1:]：接着，删除矩阵的第一列。这一列包含了原方阵的剩余所有对角线元素。
.flatten()：最后，再次将矩阵扁平化。这样，得到的就是一个包含了原方阵所有非对角线元素的一维数组。

def off_diagonal(x):
    '''
    返回方阵非对角线元素的扁平（一维）视图
    '''
    n, m = x.shape
    assert n == m
    return x.flatten()[:-1].view(n - 1, m + 1)[:, 1:].flatten()

barlow_loss计算函数：

def barlow_loss(z1, z2, bn, lambd):
    '''
    返回一对特征的Barlow Twins的loss

    :param z1：第一个输入特征
    :param z2：第二个输入特征
    :param bn：应用于 z1 和 z2 的 nn.BatchNorm1d 层
    :param lambd：权衡超参数 lambda
    '''
	# 批量归一化
    z1_norm = bn(z1)
    z2_norm = bn(z2)

    batch_size = z1.size(0)

    # 计算 z1 和 z2 的协方差矩阵
    c = torch.mm(z1_norm, z2_norm.t()) / batch_size

    # loss
    c_diff = (c - torch.eye(c.size(0), device=c.device)).pow(2)
    c_diff = off_diagonal(c_diff).mul_(lambd)
    loss = c_diff.sum()

    return loss

3 整体流程

整体流程的伪代码如下：

# 训练循环
for x in loader:  # 加载一个批次包含N个样本
    # 对每个样本生成两个随机增强版本
    y_a, y_b = augment(x)  # augment函数生成数据增强版本
    
    # 计算表征
    z_a = f(y_a)  # NxD
    z_b = f(y_b)  # NxD
    
    # 沿批次维度标准化表征
    z_a_norm = (z_a - z_a.mean(dim=0)) / z_a.std(dim=0)  # NxD
    z_b_norm = (z_b - z_b.mean(dim=0)) / z_b.std(dim=0)  # NxD
    
    # 计算交叉相关矩阵
    c = torch.mm(z_a_norm.T, z_b_norm) / N  # DxD
    
    # 计算损失
    c_diff = (c - torch.eye(D, device=c.device)).pow(2)  # DxD
    # 将非对角线元素乘以lambda
    off_diagonal(c_diff).mul_(lambda_off_diag)
    loss = c_diff.sum()
    
    # 优化步骤
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()